スマイルゼミとRISU算数の最大の違いは?

スマイルゼミとRISU算数。どちらも専用タブレットを使って学習します。どちらも幼児向けコース「すまいるぜみ」「RISUきっず」があることも共通しています。
ではスマイルゼミとRISUはどう違うか?
最大の違いは教科の種類です!
まずスマイルゼミは、国語・算数・英語・理科・社会などの教科学習全般をカバーしています。タブレット学習で学校での学習に備えるというのが基本の使い方と言ってよいでしょう。
詳細記事 スマイルゼミ小学生コース体験口コミ⇒
詳細記事 スマイルゼミ幼児コース体験口コミ⇒
詳細記事 スマイルゼミ年少コース体験口コミ⇒
一方、RISU算数/RISUきっずは算数に特化しています。
詳細記事 RISU算数体験口コミ⇒
詳細記事 RISUきっず体験口コミ⇒
「教科学習全般に取り組みたいならスマイルゼミ。特に算数に力を入れたいならRISU」と考えれば、どちらを選べばよいか、簡単に決められますね。
なお、他の通信教育との比較はこちらをご覧ください。
関連記事 小学生通信教育14社比較⇒
関連記事 無学年学習ができる通信教育10社比較⇒
関連記事 幼児通信教育15選比較⇒
スマイルゼミ・コアトレとRISU算数を比較

教科の種類に注目すれば、スマイルゼミとRISU算数のどちらがご家庭に合っているか、簡単に決められます。とは言ったものの……

2022年からは、どちらが良いかの判断が難しくなりました!
2022年4月、スマイルゼミに無学年学習「コアトレ」が登場しました。幼児コース・小学生コースのどちらも、算数と国語の先取り学習を、なんと中学3年範囲までできるようになったのです!これはとても画期的!追加料金はかかりません。
RISU算数も無学年学習です。自分の学年に関係なく、算数の先取り学習ができることが強みです。
詳細記事 RISU算数による先取り学習⇒
2022年以前は、算数の先取り学習といえば、RISU算数の一人勝ちという印象がありました。RISU算数は、受講者の約75%が、自分よりも上の学年を先取り学習しています。「算数で周囲よりどんどん先に進みたければRISU一択」という感じでした。
しかしながら、コアトレの登場で、算数の先取り学習をしたい人は、RISU算数の代わりにスマイルゼミという選択肢もできたのです。

これはちょっと悩ましい!
そこで、この記事では、算数の先取り学習にポイントを当てて、スマイルゼミとRISU算数を比較してみます。
スマイルゼミ・コアトレは中3範囲まで
スマイルゼミ・コアトレでは、算数(数学)と国語の先取り学習を中学3年範囲まで取り組むことができます。
算数(数学)では、【計算/数量/図形】の3分野を扱います。つまり「全部」です。中3までのほぼすべての単元が、14のステージに分かれて構成されています。
| ステージ | 分野 | 単元 |
|---|---|---|
| 1 | 計算 | 数を比べよう |
| 1 | 計算 | 10までの数 |
| 1 | 計算 | 数を書こう |
| 1 | 計算 | いくつといくつ(1) |
| 1 | 計算 | いくつといくつ(2) |
| 1 | 計算 | 何番目 |
| 1 | 計算 | 20までの数 |
| 1 | 計算 | 60までの数 |
| 1 | 数量 | 長さと水のかさ |
| 1 | 数量 | 時計 |
| 2 | 計算 | 120までの数 |
| 2 | 計算 | 足し算 |
| 2 | 計算 | 引き算 |
| 2 | 計算 | くり上がり・くり下がり |
| 2 | 計算 | 3つの数の計算 |
| 2 | 計算 | 足し算と筆算 |
| 2 | 計算 | 引き算と筆算 |
| 2 | 計算 | 1000までの数 |
| 2 | 数量 | 表とグラフ |
| 2 | 図形 | 形 |
| 3 | 計算 | 足し算の筆算 |
| 3 | 計算 | 引き算の筆算 |
| 3 | 計算 | かけ算(1) |
| 3 | 計算 | かけ算(2) |
| 3 | 計算 | かけ算(3) |
| 3 | 計算 | 1万までの数 |
| 3 | 数量 | 長さ |
| 3 | 数量 | 水のかさ |
| 3 | 数量 | 時刻と時間 |
| 3 | 図形 | いろいろな形 |
| 4 | 計算 | 大きい数の足し算 |
| 4 | 計算 | 大きい数の引き算 |
| 4 | 計算 | かけ算の利用 |
| 4 | 計算 | わり算・わり算の利用 |
| 4 | 計算 | あまりのあるわり算 |
| 4 | 計算 | 1億までの数 |
| 4 | 計算 | 1桁の数をかける筆算 |
| 4 | 計算 | 2桁までの数をかける かけ算の筆算 |
| 5 | 計算 | 小数の表し方 |
| 5 | 計算 | 小数の計算 |
| 5 | 計算 | 分数の表し方 |
| 5 | 計算 | 分数の計算 |
| 5 | 数量 | 長い長さ |
| 5 | 数量 | 重さ |
| 5 | 図形 | 円と球 |
| 5 | 図形 | 三角形と角 |
| 6 | 計算 | 1億より大きい数 |
| 6 | 計算 | 大きい数のかけ算 |
| 6 | 計算 | 1桁の数で割る筆算 |
| 6 | 計算 | 2桁の数で割る筆算(1) |
| 6 | 計算 | 2桁の数で割る筆算(2) |
| 6 | 計算 | 計算の決まり |
| 6 | 計算 | 概数 |
| 7 | 計算 | 小数と整数のわり算 (小数第二位) |
| 7 | 計算 | 小数の表し方 (小数第二位まで) |
| 7 | 計算 | 小数の足し算・引き算 (小数第二位まで) |
| 7 | 計算 | 小数と整数のかけ算 (小数第二位まで) |
| 7 | 計算 | いろいろな数の計算 |
| 7 | 数量 | 表とグラフ |
| 7 | 図形 | 図形 |
| 7 | 図形 | 直方体と立方体 |
| 8 | 計算 | 偶数と奇数/倍数と約数 |
| 8 | 計算 | 分数と小数と整数 |
| 8 | 計算 | 分数の足し算・引き算(通分) |
| 8 | 計算 | 帯分数の足し算・引き算(通分) |
| 8 | 数量 | 変わり方 |
| 8 | 数量 | 平均と単位量あたりの大きさ |
| 8 | 図形 | 正方形と長方形の面積 |
| 8 | 図形 | 直方体・立方体の体積 |
| 8 | 図形 | いろいろな図形の面積 |
| 9 | 計算 | 小数をかけるかけ算 |
| 9 | 計算 | 小数でわるわり算 |
| 9 | 計算 | 小数でわるわり算の利用 |
| 9 | 数量 | 速さ |
| 9 | 数量 | 割合 |
| 9 | 数量 | 帯グラフ・円グラフ |
| 9 | 数量 | 比 |
| 9 | 数量 | 比例 |
| 9 | 数量 | 反比例 |
| 10 | 計算 | 分数のかけ算 |
| 10 | 計算 | 分数のわり算 |
| 10 | 計算 | 分数のかけ算・ わり算の利用(1) |
| 10 | 計算 | 分数のかけ算・ わり算の利用(2) |
| 10 | 図形 | 図形と角 |
| 10 | 図形 | 図形と合同 |
| 10 | 図形 | 円周と円の面積 |
| 11 | 計算 | 文字を使った式 |
| 11 | 数量 | 並べ方と組み合わせ方 |
| 11 | 数量 | いろいろな表とグラフ |
| 11 | 図形 | 角柱や円柱 |
| 11 | 図形 | 角柱や円柱の体積 |
| 11 | 図形 | 対象な図形 |
| 11 | 図形 | 拡大図と縮図 |
| 12 | 計算 | 正負の数の計算(加減) |
| 12 | 計算 | 正負の数の計算(乗除) |
| 12 | 計算 | 文字式 |
| 12 | 計算 | 一次方程式 |
| 12 | 計算 | 一次方程式の利用 |
| 12 | 数量 | 比例と反比例 |
| 12 | 図形 | 平面図形 |
| 12 | 図形 | 空間図形 |
| 13 | 計算 | 式の計算(1) |
| 13 | 計算 | 式の計算(2) |
| 13 | 計算 | 連立方程式 |
| 13 | 計算 | 連立方程式の文章題 |
| 13 | 数量 | 一次関数(1) |
| 13 | 数量 | 一次関数(2) |
| 13 | 数量 | 確率 |
| 13 | 図形 | 平行と合同 |
| 13 | 図形 | 三角形と四角形 |
| 14 | 計算 | 多項式 |
| 14 | 計算 | 素因数分解・因数分解 |
| 14 | 計算 | 平方根 |
| 14 | 計算 | 二次方程式 |
| 14 | 計算 | 二次方程式の文章題 |
| 14 | 数量 | 二乗に比例する関数 |
| 14 | 図形 | 相似 |
| 14 | 図形 | 円周角 |
| 14 | 図形 | 三平方の定理 |
RISUには中学受験基礎・中学数学もあり
RISU算数では、小1~6年レベルの算数全般に取り組むことができます。スマイルゼミ・コアトレと同様【計算/数量/図形】など算数の全分野を、RISU算数では94ものステージに分けてカバーしています。
RISU算数 低学年ステージ表
RISU算数 高学年ステージ表
小6範囲までを完了したら、「受験基礎レベル」に進むこともできます。受験基礎レベルでは、中学受験に向けて、「植木算」「流水算」などの中学受験特有の問題に取り組みます。
| ステージ | 学習内容 |
|---|---|
| 1 | つるかめ算と過不足算 |
| 2 | 虫食い算 |
| 3 | 植木算 |
| 4 | 旅人算 |
| 5 | インド式暗記術 |
| 6 | 規則性の問題 |
| 7 | さまざまな数列 |
| 8 | 場合の数と確立 |
| 9 | 和差算&分配算 |
| 10 | あざやかに解ける計算 |
| 11 | 仕事算 |
| 12 | 相当算 |
| 13 | 入試でラストステージ! |
中学受験基礎ステージを完了したら、さらに「数学コース」に進むこともできます。数学コースは2025年3月にリリースされた新コンテンツ。中学1~3年内容全般の学習です。
関連記事 【RISU数学体験口コミ】中学数学先取り学習を小学生ができる?!⇒
数学コースは、中学数学の基礎を学ぶ「数学Basic」、「代数」「幾何」「統計」の4分野で構成されています。「数学Basic」を終えたら、残りの3分野については好きなものを選んで、掘り下げて取り組めるようになっています。
| ステージ | ステージ名 | 相当学年 |
|---|---|---|
| 1 | 正負の数 | 中1 |
| 2 | 正負の数のたし算・ひき算① | 中1 |
| 3 | 正負の数のたし算・ひき算② | 中1 |
| 4 | 正負の数のかけ算 | 中1 |
| 5 | 正負の数のわり算 | 中1 |
| 6 | 累乗ってなんだろう | 中1 |
| 7 | 正負の数の四則計算 | 中1 |
| 8 | 2重・3重カッコの計算 | 中1 |
| 9 | 正負の数 まとめ | 中1 |
| 10 | 累乗と素因数分解 | 中1 |
| 11 | 平方根の基礎 | 中3 |
| 12 | 平方根の計算 | 中3 |
| 13 | 有理数と無理数 | 中3 |
| ステージ | ステージ名 | 相当学年 |
|---|---|---|
| 1 | 文字式① 文字式って? | 中1 |
| 2 | 文字式② 四則計算 | 中1 |
| 3 | 文字式③ 応用の練習 | 中1 |
| 4 | 1次方程式① 方程式って? | 中1 |
| 5 | 1次方程式② 解を出そう! | 中1 |
| 6 | 1次方程式③ 計算練習 | 中1 |
| 7 | 1次方程式④ 計算の工夫 | 中1 |
| 8 | 1次方程式⑤ 文章題 | 中1 |
| 9 | 多項式について学ぼう! | 中1 |
| 10 | 連立方程式:代入法 | 中2 |
| 11 | 連立方程式:加減法 | 中2 |
| 12 | 連立方程式の応用① | 中2 |
| 13 | 連立方程式:計算の工夫 | 中2 |
| 14 | 連立方程式の応用② | 中2 |
| 15 | 応用問題を数学で解こう! | 中2 |
| 16 | 難関中学入試を数学で解こう! | 中2 |
| 17 | 不等式の性質と解 | 高1 |
| 18 | 連立不等式 | 高1 |
| 19 | 不等式の利用 | 高1 |
| 20 | 単項式と多項式 | 中2 |
| 21 | 単項式の乗除 | 中2 |
| 22 | 文字式の利用 | 中2 |
| 23 | 式の計算① 多項式 | 中3 |
| 24 | 式の計算② さまざまな展開 | 中3 |
| 25 | 式の計算③ 因数分解の基本 | 中3 |
| 26 | 式の計算④ 因数分解の工夫 | 中3 |
| 27 | 式の計算⑤ 式の計算の利用 | 中3 |
| 28 | 1次関数① 比例 | 中1 |
| 29 | 1次関数② 比例のグラフ | 中1 |
| 30 | 1次関数③ 反比例とグラフ | 中1 |
| 31 | 1次関数④ 比例の利用 | 中1 |
| 32 | 1次関数⑤ 1次関数とグラフ | 中2 |
| 33 | 1次関数⑥ 式の求め方 | 中2 |
| 34 | 1次関数⑦ 1次関数と方程式 | 中2 |
| 35 | 1次関数⑧ 1次関数の利用 | 中2 |
| 36 | 2次方程式① 解の求め方 | 中3 |
| 37 | 2次方程式② 解の公式 | 中3 |
| 38 | 2次方程式③ 2次方程式の利用 | 中3 |
| 39 | 関数y=ax2のグラフ | 中3 |
| 40 | 関数y=ax2変化の割合 | 中3 |
| 41 | 関数y=ax2の利用 | 中3 |
| 42 | 関数y=ax2 放物線と直線 | 中3 |
| ステージ | ステージ名 | 相当学年 |
|---|---|---|
| 1 | 平面図形の基礎 | 中1 |
| 2 | 平面図形の移動 | 中1 |
| 3 | 平面図形の作図 | 中1 |
| 4 | 面積を求めよう | 中1 |
| 5 | 直線と平面の位置関係 | 中1 |
| 6 | 立体のいろいろな見方 | 中1 |
| 7 | 立体の体積と表面積 | 中1 |
| 8 | 立体図形の応用問題 | 中1 |
| 9 | 平行線と角 | 中2 |
| 10 | 多角形の内角と外角 | 中2 |
| 11 | 三角形の合同と証明 | 中2 |
| 12 | 二等辺三角形の定理と証明 | 中2 |
| 13 | 直角三角形の合同と証明 | 中2 |
| 14 | 平行四辺形の定理と証明 | 中2 |
| 15 | 様々な四角形の証明 | 中2 |
| 16 | 三平方の定理 | 中3 |
| 17 | 三平方の定理の利用 | 中3 |
| 18 | 三平方の定理と立体 | 中3 |
| 19 | 相似① 相似な図形 | 中3 |
| 20 | 相似② 平行線と線分の比 | 中3 |
| 21 | 相似③ 面積比、体積比 | 中3 |
| 22 | 相似④ 相似の利用 | 中3 |
| 23 | 円① 円と三角形 | 中3 (一部高校) |
| 24 | 円② 円周角の定理 | 中3 |
| 25 | 円③ 円に内接する図形 | 中3 |
| 26 | 円④ 接線と方べきの定理 | 中3 |
| ステージ | ステージ名 | 相当学年 |
|---|---|---|
| 1 | 代表値・階級・度数 | 中1 |
| 2 | 相対度数と累積度数 | 中1 |
| 3 | 四分位置と箱ひげ図 | 中2 |
| 4 | 母集団と標本 | 中3 |
| 5 | 母集団の推定とバイアス | 中3 |
| 6 | 場合の数 | 中2 |
| 7 | 確率を求めてみよう | 中2 |
| 8 | 順列と組み合わせ | 中2 |
| 9 | 事柄の起こりやすさと確立 | 中2 |
どちらも中学3学年分を先取りできる。
算数(数学)の先取り学習という点でスマイルゼミとRISU算数を比較した場合、先取り学習の範囲については、以前は中3範囲までカバーしているスマイルゼミの方が勝っていました。
しかし「数学コース」のリリースで、RISU算数でも中学3学年分の数学をガッツリ学習できるようになりました。ですので先取り範囲の点では、スマイルゼミとRISU算数は甲乙つけがたいです。
両方とも中学3学年分の先取り学習ができるものの、RISUなら「代数」だけ、「幾何」だけといった取り組みも可能です。その点で、RISUの方が使いやすいと言えるかもしれません。
スマイルゼミ・コアトレとRISU算数の難易度比較

スマイルゼミ・コアトレとRISUを難易度で比較してみましょう。

スマイルゼミ・コアトレは基礎力強化を重視
スマイルゼミ・コアトレでは、「計算」「数量」「図形」を学習します。ですが、コアトレの軸は「計算」です。
ここで再度コアトレのステージ表を見てみましょう。
| ステージ | 分野 | 単元 |
|---|---|---|
| 1 | 計算 | 数を比べよう |
| 1 | 計算 | 10までの数 |
| 1 | 計算 | 数を書こう |
| 1 | 計算 | いくつといくつ(1) |
| 1 | 計算 | いくつといくつ(2) |
| 1 | 計算 | 何番目 |
| 1 | 計算 | 20までの数 |
| 1 | 計算 | 60までの数 |
| 1 | 数量 | 長さと水のかさ |
| 1 | 数量 | 時計 |
| 2 | 計算 | 120までの数 |
| 2 | 計算 | 足し算 |
| 2 | 計算 | 引き算 |
| 2 | 計算 | くり上がり・くり下がり |
| 2 | 計算 | 3つの数の計算 |
| 2 | 計算 | 足し算と筆算 |
| 2 | 計算 | 引き算と筆算 |
| 2 | 計算 | 1000までの数 |
| 2 | 数量 | 表とグラフ |
| 2 | 図形 | 形 |
| 3 | 計算 | 足し算の筆算 |
| 3 | 計算 | 引き算の筆算 |
| 3 | 計算 | かけ算(1) |
| 3 | 計算 | かけ算(2) |
| 3 | 計算 | かけ算(3) |
| 3 | 計算 | 1万までの数 |
| 3 | 数量 | 長さ |
| 3 | 数量 | 水のかさ |
| 3 | 数量 | 時刻と時間 |
| 3 | 図形 | いろいろな形 |
| 4 | 計算 | 大きい数の足し算 |
| 4 | 計算 | 大きい数の引き算 |
| 4 | 計算 | かけ算の利用 |
| 4 | 計算 | わり算・わり算の利用 |
| 4 | 計算 | あまりのあるわり算 |
| 4 | 計算 | 1億までの数 |
| 4 | 計算 | 1桁の数をかける筆算 |
| 4 | 計算 | 2桁までの数をかける かけ算の筆算 |
| 5 | 計算 | 小数の表し方 |
| 5 | 計算 | 小数の計算 |
| 5 | 計算 | 分数の表し方 |
| 5 | 計算 | 分数の計算 |
| 5 | 数量 | 長い長さ |
| 5 | 数量 | 重さ |
| 5 | 図形 | 円と球 |
| 5 | 図形 | 三角形と角 |
| 6 | 計算 | 1億より大きい数 |
| 6 | 計算 | 大きい数のかけ算 |
| 6 | 計算 | 1桁の数で割る筆算 |
| 6 | 計算 | 2桁の数で割る筆算(1) |
| 6 | 計算 | 2桁の数で割る筆算(2) |
| 6 | 計算 | 計算の決まり |
| 6 | 計算 | 概数 |
| 7 | 計算 | 小数と整数のわり算 (小数第二位) |
| 7 | 計算 | 小数の表し方 (小数第二位まで) |
| 7 | 計算 | 小数の足し算・引き算 (小数第二位まで) |
| 7 | 計算 | 小数と整数のかけ算 (小数第二位まで) |
| 7 | 計算 | いろいろな数の計算 |
| 7 | 数量 | 表とグラフ |
| 7 | 図形 | 図形 |
| 7 | 図形 | 直方体と立方体 |
| 8 | 計算 | 偶数と奇数/倍数と約数 |
| 8 | 計算 | 分数と小数と整数 |
| 8 | 計算 | 分数の足し算・引き算(通分) |
| 8 | 計算 | 帯分数の足し算・引き算(通分) |
| 8 | 数量 | 変わり方 |
| 8 | 数量 | 平均と単位量あたりの大きさ |
| 8 | 図形 | 正方形と長方形の面積 |
| 8 | 図形 | 直方体・立方体の体積 |
| 8 | 図形 | いろいろな図形の面積 |
| 9 | 計算 | 小数をかけるかけ算 |
| 9 | 計算 | 小数でわるわり算 |
| 9 | 計算 | 小数でわるわり算の利用 |
| 9 | 数量 | 速さ |
| 9 | 数量 | 割合 |
| 9 | 数量 | 帯グラフ・円グラフ |
| 9 | 数量 | 比 |
| 9 | 数量 | 比例 |
| 9 | 数量 | 反比例 |
| 10 | 計算 | 分数のかけ算 |
| 10 | 計算 | 分数のわり算 |
| 10 | 計算 | 分数のかけ算・ わり算の利用(1) |
| 10 | 計算 | 分数のかけ算・ わり算の利用(2) |
| 10 | 図形 | 図形と角 |
| 10 | 図形 | 図形と合同 |
| 10 | 図形 | 円周と円の面積 |
| 11 | 計算 | 文字を使った式 |
| 11 | 数量 | 並べ方と組み合わせ方 |
| 11 | 数量 | いろいろな表とグラフ |
| 11 | 図形 | 角柱や円柱 |
| 11 | 図形 | 角柱や円柱の体積 |
| 11 | 図形 | 対象な図形 |
| 11 | 図形 | 拡大図と縮図 |
| 12 | 計算 | 正負の数の計算(加減) |
| 12 | 計算 | 正負の数の計算(乗除) |
| 12 | 計算 | 文字式 |
| 12 | 計算 | 一次方程式 |
| 12 | 計算 | 一次方程式の利用 |
| 12 | 数量 | 比例と反比例 |
| 12 | 図形 | 平面図形 |
| 12 | 図形 | 空間図形 |
| 13 | 計算 | 式の計算(1) |
| 13 | 計算 | 式の計算(2) |
| 13 | 計算 | 連立方程式 |
| 13 | 計算 | 連立方程式の文章題 |
| 13 | 数量 | 一次関数(1) |
| 13 | 数量 | 一次関数(2) |
| 13 | 数量 | 確率 |
| 13 | 図形 | 平行と合同 |
| 13 | 図形 | 三角形と四角形 |
| 14 | 計算 | 多項式 |
| 14 | 計算 | 素因数分解・因数分解 |
| 14 | 計算 | 平方根 |
| 14 | 計算 | 二次方程式 |
| 14 | 計算 | 二次方程式の文章題 |
| 14 | 数量 | 二乗に比例する関数 |
| 14 | 図形 | 相似 |
| 14 | 図形 | 円周角 |
| 14 | 図形 | 三平方の定理 |
「計算」「数量」「図形」の中で、「計算」が占める割合が多いのが分かりますね。スマイルゼミ・コアトレでは、「計算」で学んだことを活かして「数量」や「図形」に効率的に取り組むようにカリキュラムが組まれています。
「計算」は算数・数学の基礎ですね。「計算」を軸にすることによって基礎力をしっかり鍛えるというのが、コアトレの狙いのようです。
スマイルゼミのパンフレットには、コアトレについて次の説明があります。
一人でも理解を深めながら解き進められる仕組みで、算数・数学/国語の基礎力を鍛え、より正確に、より速く解く力を身につけます
スマイルゼミ小学生向け通信教育「入会のご案内」より引用
スマイルゼミ・コアトレの算数(数学)では、初めての内容でも動画などを見ながらしっかりと理解した後、実際にスモールステップで問題を解いていきます。そしてそのステージがクリアになっても、制限時間内で解いたり連続正解を目指したりする「トレーニング」が用意されています。
つまり、コアトレでは先取りして身に付けるだけでなく、より速く、より正確に解けるよう、強化してくれる設計になっています。
また、身に付けた計算方法を応用して取り組む文章題も豊富に出題されます。
但し、スマイルゼミ・コアトレには中学受験に直結するほどのひねった問題や高難易度の問題ははありません。あくまでも教科書レベルと考えるとよいでしょう。
学校で習っていないことでも着実に定着させ、強化してくれるのがスマイルゼミ・コアトレの算数(数学)です。
RISU算数は応用問題豊富
RISU算数でも、スマイルゼミ・コアトレと同様、動画などで学校で習っていないことでもスムーズに理解できるように設計されています。
RISU算数を利用する小学生の30%以上が苦手からのスタートなのだそう。RISUにはつまづきを感知するシステムがあり、間違いが多かった問題の復習を自動出題してくれるので、小学生が否が応でも苦手克服できる設計になっています。
RISU算数もスマイルゼミ・コアトレと同様、スモールステップで学習し、ステージをクリアしながら進んでいきます。
RISU算数で特徴的なのは、まず文章題が多いこと。RISUの教材1学年分には、国語の教科書1年分の文章量が入っているのだそう!算数を学習しながら、全ての学習の基本である国語力も伸びる仕掛けになっています。

さらにRISU算数には応用問題が豊富です。小学生がテンポよく問題を解いていると、突然「鬼モード」が発動され、高難易度の問題にチャレンジさせてくれます。
また、パズルや暗号のようなひねった問題や中学受験問題などの「スペシャル問題」も出てきます。算数オリンピックの問題も含まれているほど、手ごわい問題が登場します。

RISU算数では、じっくり考えないと解けない、思考力を鍛えてくれる応用問題が多く出題されます。
スマイルゼミ・コアトレとRISU算数の使い勝手比較


使いやすさを比べてみましょう。
開始ステージを選べるか
スマイルゼミ・コアトレもRISU算数も無学年学習。コアトレなら中3範囲まで、RISU算数なら小6範囲(小6範囲完了後は中学受験基礎・中学数学に移行可)まで、自分の学年に関係なく学習できます。
ではスタート位置はどこでしょう?どこから始めることになるのでしょうか?
スマイルゼミは復習からスタート
スマイルゼミ・コアトレでは、自分の学年よりも1学年下相当のステージから始まるよう設計されています。開始ステージを自分で選ぶことはできません。
例えばこちらは小学2年生がコアトレを始める時のステージ画面。小学1年生相当の「ステージ2」からスタートするようになっています。
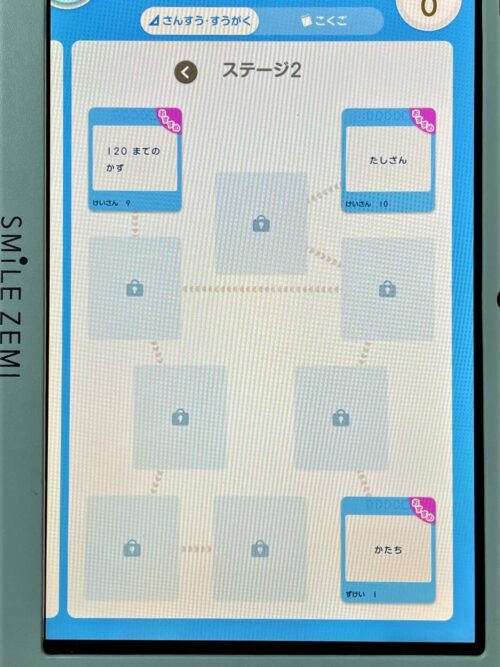
算数は「理解」しただけではダメです。計算など、その都度の単元で「正確に」「速く」できるように習熟しておかないと、あとあと力が伸びません。それが達成できるように、スマイルゼミ・コアトレでは1学年下のステージから始めるのでしょう。
スマイルゼミ・コアトレでは、あえて自分より下の学年内容から始めて、がっちり習熟できるようになっています。
RISU算数は自分に合ったステージからスタート
RISU算数では、学習開始の前に、まずタブレット上で「実力テスト」を受けます。その出来栄えによって、システムが開始ステージを決定します。
実力テストを完了すると、スキップできるステージが表示されます。

このように、RISU算数ではもう分かっている内容は飛ばして、効率よく先取り学習をスタートできるように設計されています。
手書き入力できるか
スマイルゼミもRISU算数も、専用タブレットのみで学習を進めます。
タブレット学習で気になることの1つに、端末の使いやすさがありますね。タブレットの性能については、スマイルゼミの方が勝っています。
スマイルゼミ・コアトレでは、タブレット画面に計算のメモなど自由に書き込むことができます。専用タブレットが高性能なので、ストレスなく書けます。また、選択式でなく、記述式で答える問題も多いです。

一方、RISU算数では、タブレット画面に付属のタッチペンで書き込みができはしますが、書き味はあまりよくありません。また、選択式で答えます。
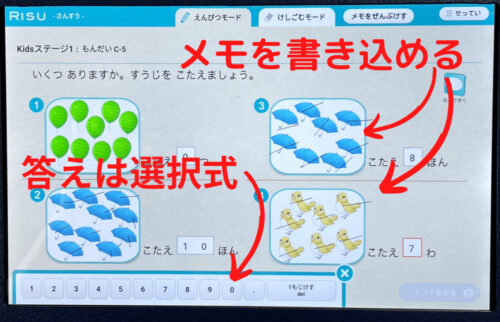
というわけで、解答する時にストレスなく「書いて」答えられるのは、断然スマイルゼミ・コアトレの方です。
RISU算数を使う場合は、計算メモなどは別の紙に書いた方がやりやすそうです。
お楽しみ要素はあるか
小学生が継続して取り組むには、何か「お楽しみ」が欲しいところ。
スマイルゼミ・コアトレのお楽しみは、なんといっても「みんトレ」でしょう。
「みんトレ」は「みんなでトレーニング」を略した言葉です。全国のスマイルゼミ・コアトレの利用者と、リアルタイムで問題の解答スピードを競い合うことができます。

「みんトレ」はリアルタイムで実在の小学生相手に行うので、オンラインゲームと似ています。小学生がゲーム感覚で楽しめます。
一方、RISU算数では取り組みを進めると「ポイント」が貯まります。このポイントを使って、プレゼントと交換することができます。
プレゼントは現物のものが多いですが、小学生に人気のプレゼントは「スペシャル鍵」なんだそう。
このスペシャル鍵は、上で紹介した「スペシャル問題」(パズルや中学入試過去問などの応用問題)にチャレンジできる権利のことです。RISU算数を始めると算数が好きになって、難しい問題に挑戦したくなる小学生が多いことが伝わってきます。
スマイルゼミ・コアトレとRISU算数の受験対策比較


中学受験をするか、高校受験をするかによっても、スマイルゼミとRISU算数のどちらがよいかが決まってきます。
高校受験準備ならスマイルゼミ
スマイルゼミは教科書準拠教材です。基本的には、学校の授業にそって予習・復習を行い、教科書レベルの定着と学力アップを目指している小学生におすすめの通信教育です。
スマイルゼミには、標準クラスのほかに発展クラスもあり、教科書を超えた学びもできます。しかしながら、それが直接中学受験対策になるというわけではありません。
スマイルゼミで学習を続けていくと、小学6年生の12月~3月には「中学準備講座」が配信されます。算数・国語・理科・社会の小学校での学習の総復習をして、中学で好スタートを切れるようにしてくれます。また中学英語の先取りをする講座も配信されるので、周りより一歩進んだ状態で中学英語を始めることができます。
つまり、スマイルゼミで学習を続けていけば、中学での学びに万全に備えられるというわけです。そしてそれは当然、3年後の高校受験にもつながっていきます。
スマイルゼミ・コアトレについて言えば、小学生のうちに中学範囲の数学・国語の先取りをしておくことができます。特に数学の得意・不得意は受験を大きく左右します。コアトレで数学を先取りしておけば、高校受験でかなり有利になります!
中学は公立中に行き、高校受験を予定しているご家庭にとっては、小学生のうちからスマイルゼミを利用することで、高校受験に万全に備えられることにも繋がっていくはずです。
中学受験準備ならRISU算数
RISU算数について注目すべきは、RISU受講者から、大手中学受験塾での模試日本一や、難関中学合格者や多数出ていることです。
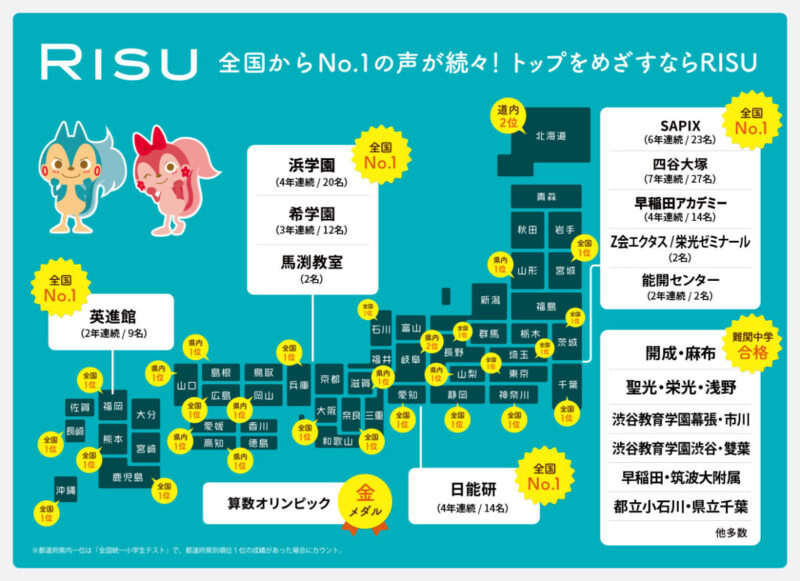
RISU算数を受講して中学受験に成功しているご家庭では、中学受験勉強が本格化する小4頃までに、RISUで小6までの教科書レベルの算数を終わらせるという戦略をとることが多いのだそう。
詳細記事 【RISU算数と中学受験】なぜRISUに難関中学合格の効果があるの?⇒
算数は中学受験の要の教科とも言えます。RISUでの先取りで教科書レベルを早期に終わらせたら、残りの期間を中受特有の特殊算などに注力できます。また、算数が得意になっていれば、他教科に余裕をもって時間を割くことができます。
中学受験を考えているご家庭は、RISU算数をぜひ検討してみるとよいと思います。
スマイルゼミとRISU算数の料金比較


気になる料金について、スマイルゼミとRISUを比較してみましょう。
まず、スマイルゼミのコアトレは追加料金0円のサービスです。スマイルゼミ受講者ならば、誰もが自由に使うことができます。幼児コースも同様です。
ですので、スマイルゼミについて以下で紹介する料金は、コアトレ込みの、通常講座の金額ということになります。
RISUは契約時に12ヶ月分を一括払いするので、スマイルゼミも12ヶ月一括場合の場合で比較します。
幼児コースの場合
| すまいるぜみ | RISUきっず | |
|---|---|---|
| 基本料金(税込) | 43,560円 月あたり3,630円 | 35,376円 月あたり2,948円 |
| タブレット代 | 10,978円 | 無料 |
幼児コースで比較すると、RISUきっずの方がお安いです。(すまいるぜみは算数だけでなく総合的な学習なので、一概に比較はできませんが) RISUは2024年9月に値上げされたのですが、それでも、すまいるぜみよりはお安くなっています。
RISUきっずのステージを全てクリアすると、自動的にRISU算数ステージ1へと移行します。
一方、すまいるぜみでは、購入したタブレットを小学講座でも引き続き使用します。幼児コース「すまいるぜみ」からスタートする場合、小学コースでのタブレットの買い替えは不要です。
小学生コースの場合
スマイルゼミには標準クラスと発展クラスがあります。発展クラスの方が講座数が多い分、料金も高くなっています。またどちらも追加料金0円で、コアトレを利用できます。
RISU算数の料金システムは複雑です。基本料金年間35,376円(税込)の他に「利用料」がかかります。利用料は、1ヵ月あたりの平均クリアステージ数によって決まります。ゆっくり学習するなら利用料金0円で済みますが、たくさん先取りすればするほど、その分、利用料が高くなります。(上限金額あり)。
受講者平均速度は、月あたり1.7~2ステージ未満クリア(学校の1.3~1.5倍速)だそう。その場合の利用料は3,828円/月(税込)です。基本料金と合わせると、月あたり6,776円かかることになります。ちょっとお高い印象を受けますね。
そこで、ここではRISU算数を小1から始めて、受講者平均速度で進んだと仮定して計算してみます。受講者平均速度でこなせば、4年程で小学6年範囲までの全ステージクリアになります。
スマイルゼミは12ヵ月一括払い(税込)の場合です。
| スマイルゼミ 標準クラス | スマイルゼミ 発展クラス | RISU算数 平均的スピード | |
|---|---|---|---|
| 端末代金 | 10,978円 | 10,978円 | 無料 |
| 小1 | 43,560円 3,630円/月 | 50,150円 4,180円/月 | 基本料35,376円 利用料45,936円 6,776円/月 |
| 小2 | 48,840円 4,070円/月 | 59,400円 4,950円/月 | 基本料35,376円 利用料45,936円 6,776円/月 |
| 小3 | 60,720円 5,060円/月 | 71,280円 5,940円/月 | 基本料35,376円 利用料45,936円 6,776円/月 |
| 小4 | 71,280円 5,940円/月 | 81,840円 6,820円/月 | 基本料35,376円 利用料45,936円 6,776円/月 |
| 小5 | 83,160円 6,930円/月 | 93,720円 7,810円/月 | ー |
| 小6 | 89,760円 7,480円/月 | 100,320円 8,360円/月 | ー |
| 合計 | 408,298円 | 467,688円 | 325,248円 |
このように、小6範囲までRISU受講者の平均的なスピードで先取りすることを想定すると、4年間で終了します。そして、合計金額はスマイルゼミよりもお安くなります。
RISU算数は月あたり6,776円となかなか高額です。でもそれは、こなすステージ数が多いから。先取りによって全ステージを早く完了することになるので、結果的にはそれほど高くないことが分かりますね。
もっともスマイルゼミ・コアトレでは国語の先取りもできるので、算数・数学だけの先取りができるRISU算数の方がお安いとも言い切れません。また、スマイルゼミでは算数だけでなく学習全般をカバーしていることも考慮すると、スマイルゼミの方がお得感はあります。
スマイルゼミとRISU算数比較まとめ

スマイルゼミとRISU算数は結局どちらがよいでしょうか?
スマイルゼミとRISU算数は、それぞれの強みや魅力があります。併用するご家庭もあるほどです。次のようなポイントで考えると、どちらがよいか決めやすいと思います。

元中学校教師で現在プロ家庭教師。家庭教師という職業柄、ご家庭からお子さんの家庭学習について相談を受けることが多い。そこで、様々な最新の通信教材を実際に手にしたり自分で受講して精査し、ご家庭にアドバイス。その教材研究や経験に基づいて、この記事を執筆しました。





コメント